Unveiling quantum phase transitions from traps in variational quantum algorithms
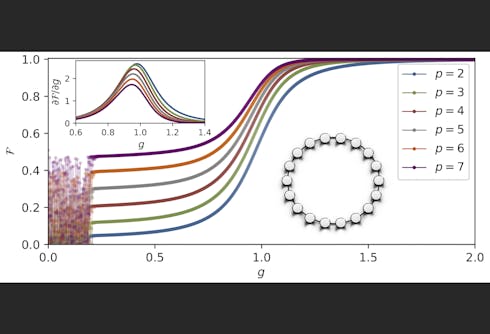
Understanding quantum phase transitions in physical systems is fundamental to characterize their behaviour at small temperatures. Achieving this requires both accessing good approximations to the ground state and identifying order parameters to distinguish different phases. Addressing these challenges, our work introduces a hybrid algorithm that combines quantum optimization with classical machine learning. This approach leverages the capability of near-term quantum computers to prepare locally trapped states through finite optimization. Specifically, we utilize LASSO for identifying conventional phase transitions and the Transformer model for topological transitions, applying these with a sliding window of Hamiltonian parameters to learn appropriate order parameters and estimate the critical points accurately. We verified the effectiveness of our method with numerical simulation and real-hardware experiments on Rigetti's Ankaa 9Q-1 quantum computer. Our protocol not only provides a robust framework for investigating quantum phase transitions using shallow quantum circuits but also significantly enhances efficiency and precision, opening new avenues in the integration of quantum computing and machine learning.